A Simplified Explanation Of The New Kolmogorov-Arnold Network (KAN) from MIT

🌈 Abstract

Exploring the Next Frontier in AI: The Kolmogorov-Arnold Network (KAN)

🙋 Q&A

[01] Kolmogorov-Arnold Network (KAN)

1. What is the Kolmogorov-Arnold Network (KAN)?

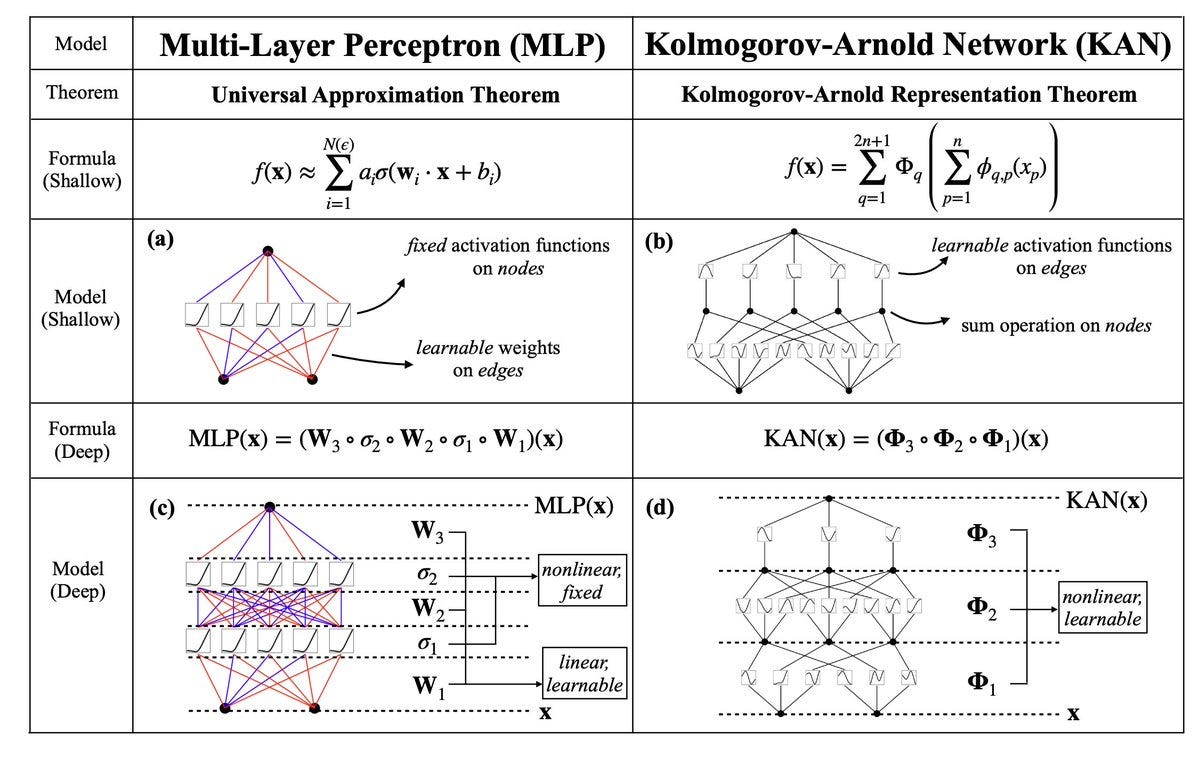
• KAN is a new architecture in artificial intelligence developed at MIT that aims to transform traditional neural network models.
• KAN redefines the role and operation of activation functions, incorporating univariate functions that act as both weights and activation functions, which can adapt as part of the learning process.

2. How does KAN differ from traditional Multi-Layer Perceptrons (MLPs)?

• Unlike the static, non-learnable activation functions in MLPs, KAN allows the activation functions to be learned as part of the training process.
• KAN moves the activation functions to the edges of the network rather than the neuron's core, potentially altering learning dynamics and enhancing interpretability.
• KAN applies non-linearity before summing inputs, allowing differentiated treatment of features and potentially more precise control over input influence on outputs.

3. What are the potential benefits of the KAN architecture?

• KAN could lead to networks that are fundamentally more capable of handling complex, dynamic tasks compared to traditional neural network models.
• The innovative architecture of KAN may enhance the interpretability and efficiency of neural network operations.

[02] Comparison to Multi-Layer Perceptrons (MLPs)

1. What is the traditional structure of Multi-Layer Perceptrons (MLPs)?

• MLPs structure computations through layered transformations, where inputs are processed by multiplying them with weights, adding a bias, and applying an activation function.
• The essence of training these networks lies in optimizing the weights (W) to enhance performance for specific tasks.

2. How does the KAN architecture differ from the traditional MLP approach?

• KAN introduces a radical shift from the MLP paradigm by redefining the role and operation of activation functions.
• In KAN, the activation functions are not static and non-learnable as in MLPs, but rather they are univariate functions that can adapt as part of the learning process.

3. What are the key differences between the mathematical representations of KAN and MLPs?

• In a simplified KAN representation, the output is calculated as f(x1, x2) = Φ2(φ2,1(φ1,1(x1) + φ1,2(x2))), where the φ functions are the learnable univariate activation functions.
• In contrast, the traditional MLP representation is f(x) = σ (W * x + B), where σ is the fixed activation function, W are the weights, and B is the bias.