The Gambler's Fallacy is Not a Fallacy

🌈 Abstract

The article discusses the rationality of the "gambler's fallacy" - the tendency to think that if an event has recently happened more frequently than normal, it's less likely to happen in the future. The author argues that this "fallacy" is actually rational in many cases, given people's limited knowledge about the statistical mechanisms underlying random processes.

🙋 Q&A

[01] The Gambler's Fallacy

1. What is the gambler's fallacy? The gambler's fallacy is the tendency to think that if an event has recently happened more frequently than normal, it's less likely to happen in the future. This is considered an irrational belief.

2. What is the author's main claim about the gambler's fallacy? The author argues that the gambler's fallacy is actually rational in many cases, given people's limited knowledge about the statistical mechanisms underlying random processes.

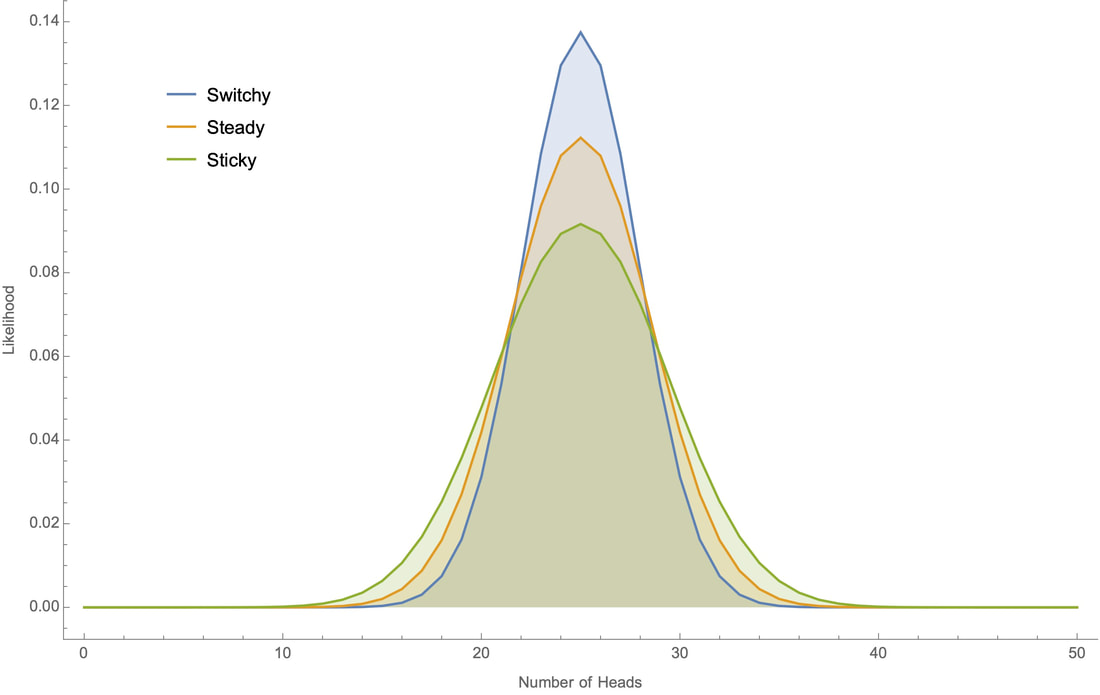
3. What are the key hypotheses the author considers about the underlying statistical mechanisms? The author considers three hypotheses about the underlying statistical mechanisms:

• Steady: The chance of heads is always 50%
• Switchy: The coin has a tendency to switch between heads and tails
• Sticky: The coin has a tendency to stick to how it has been landing

4. How does the author show that committing the gambler's fallacy can be rational? The author shows that if you are uncertain between the Switchy and Sticky hypotheses, and you know the coin lands heads around 50% of the time, then you should be more confident in the Switchy hypothesis. This means you should commit the gambler's fallacy and think a heads is more likely after a streak of tails.

5. What is the key insight behind the author's argument? The key insight is that people often don't (and can't) have full information about the statistical mechanisms underlying the random processes they encounter. As long as they leave open the possibility of Switchy or Sticky hypotheses, committing the gambler's fallacy can be a rational response.

[02] The Gambler's Fallacy in Real Life

1. How does the author's argument about koins generalize to real-life random processes? The author argues that many real-life random processes, like weather, social media engagement, etc. are also plausibly either Switchy or Sticky. So people who don't have full information about the underlying statistical mechanisms should often commit the gambler's fallacy rationally.

2. What is the author's response to the objection that coins have no "memory" so the gambler's fallacy should not apply? The author argues that even for coins, the way real people tend to flip them can lead to Switchy or Sticky behavior, rather than the idealized Steady hypothesis. So people without detailed knowledge of coin flipping should still leave open the possibility of Switchy/Sticky hypotheses.

3. What is the author's overall conclusion about the gambler's fallacy? The author concludes that the mere fact that people exhibit the gambler's fallacy does not necessarily show irrationality. Rather, it may reveal a subtle sensitivity to statistical uncertainty, given people's limited knowledge about the random processes they encounter.